Parallel Tempering
After a few days of working out the bugs in between other projects, I now have the spot modeling code working with parallel tempering. Briefly, parallel tempering allows for better exploration of the parameter space of multi-modal distributions. In my particular example, there may be (and probably are) many spots on the surface of a star. I am trying to find the most probable coordinates for the spots, as well as their sizes, and other properties of the star. When performing the normal Affine Invariant MCMC Ensemble sampling of emcee, Markov chains will get stuck in local minima (e.g. smaller spot locations), and do not explore the full parameter space to find the larger spot locations. Parallel tempering reduces the height of the barriers between the posterior distribution, allowing chains to fully explore the parameter space, and find the dominant spot locations.
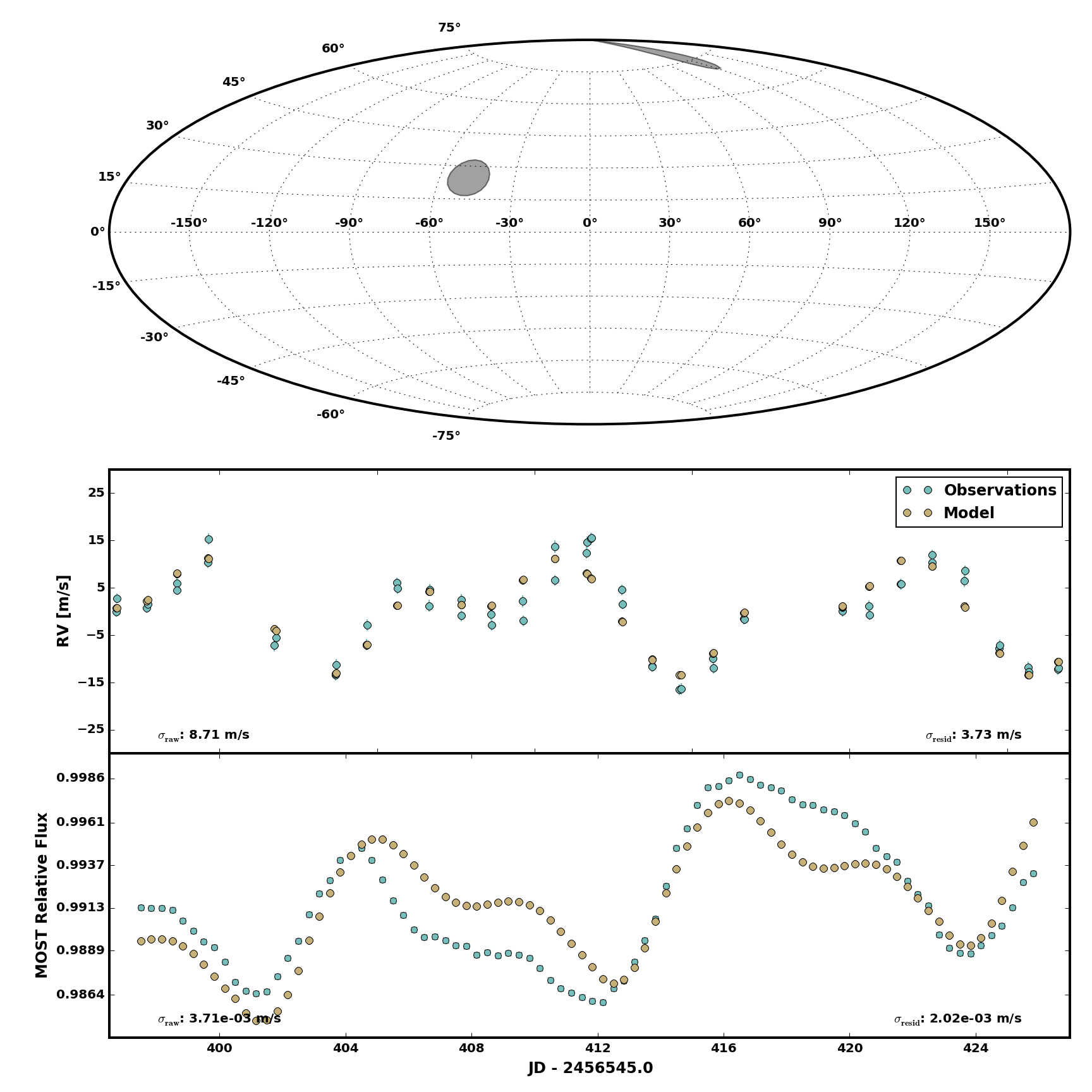
Here is the best fit solution employing a maximum likelihood method with an excellent initial guess based on a grid search:
And here are 100 random samples taken from the parallel tempering method:
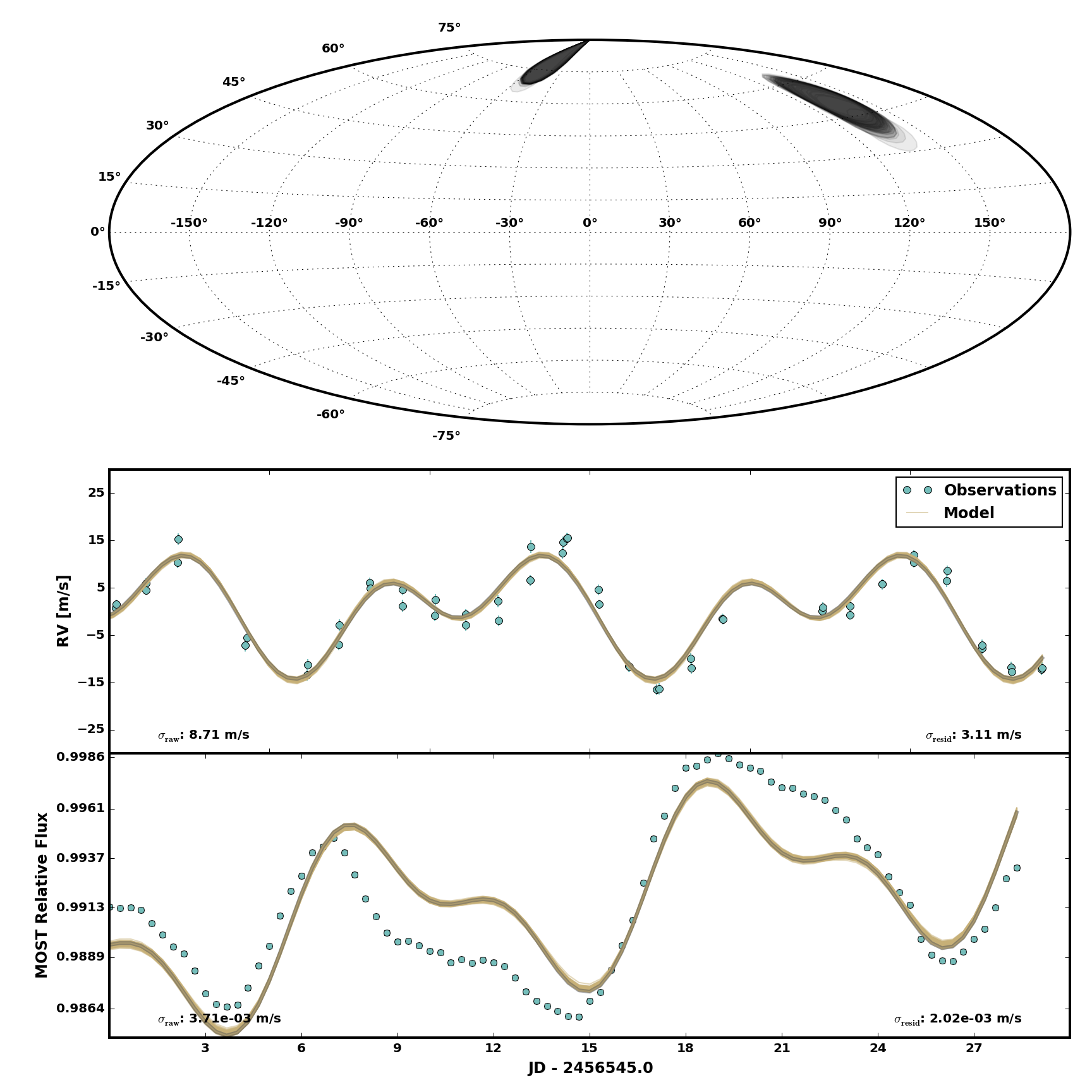
Note the standard deviation of the residuals for the photometry is unchanged, but the standard deviation of the residuals for the RV data benefited from a 62 cm/s improvement.